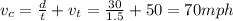Question

A car and a truck are moving in the same direction on the same highway. The truck is moving at 50mph and car is traveling at a constant speed. At 3:00pm,the car is 30miles behind the truck and at 4:30pm the car overtake and passes the truck. What is the speed of the car?

​

Answer 1

70 mph

Step-by-step explanation:

We can write the position of the car at time t as

`x_c (t) = v_c t`

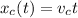
where
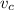`v_c` is the speed of the car, while the position of the truck is

`x_t (t) = d + v_t t`

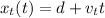
where

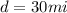`d = 30 mi` is the initial distance between the car and the truck (at 3:00 pm)

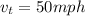`v_t = 50 mph` is the speed of the truck

The car overcomes the truck when they have same position, so

`x_c = x_t\\v_c t = d + v_t t`

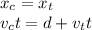
This occurs at 4:30 pm, so 1:30 h (1.5 h) after the initial instant. So, by using

t = 1.5 h

And solving the equation for
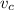`v_c`, we find the speed of the car:

`v_c =(d)/(t)+v_t=(30)/(1.5)+50=70 mph`