Answer:
Option 3 -
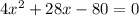
Explanation:
We have given,
The length of a rectangular frame is represented by the expression L=2x+4.
The width of the rectangular frame is represented by the expression B=2x+10.
The total area of a rectangular frame is A=120 square inches.
To find : Write an equation to solve for the width of a rectangular frame ?
Solution :
The area of the rectangle is given by,
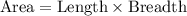
Substitute the values,

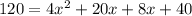
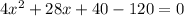
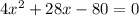
The required equation is
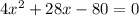
Therefore, option 3 is correct.