Question

Two bolls with a masses m and 2m are connected by a rod of negligible mass. The rod can be rotated in several positions along the rod. To obtain the greatest angular accretion for a fix torque applied Determine the position of the torque applied to obtaim the greatest angular acceleration 2m.

Answer 1

\alpha = \frac{2F}{3m} \ \frac{1}{r}

maximmun x =r

Step-by-step explanation:

In this exercise we are asked for the maximum angular acceleration, let's start by writing the second law of / newton for rotational motion. Let's fix our reference system at the midpoint of the bar that has a length 2r

Σ τ = (I₁ + I₂) α

where I₁ and I₂ moment of inertia of the capsule with masses m and 2m, respectively. Let's treat these capsules as point particles

I₁ = m r²

I₂ = 2m r²

the troque of a pair of force is the force times the distance perpendicular to the point of application of the force which is the same for both forces, we will assume that the counterclockwise rotation is positive

Στ = F x + F x

the angular acceleration is the same because they are joined by the bar of negligible mass, let us substitute

2 F x = (m r² + 2m r²) α

α =
`(2F x)/(3m r^(2) )`

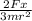
α =
`(2F )/(3m ) \ (x)/(r^(2) )`

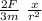
let's analyze this expression

* for the application point in the center (x = 0) at acceleration is zero

* for the point of application of the torque at the ends the acceleration is

`\alpha = (2F)/(3m) \ (1)/(r)`

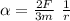
this being its maximum value