Answer:
UCL = 14.624
Step-by-step explanation:
Data Given:
z= 3
And beside the value of z, we are given:
Number of samples = 5
And observations.
First of all, we have to calculate the mean of all the samples.
Sample 1 Mean =
 = 12
= 12
Sample 2 Mean =
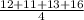 = 13
= 13
Sample 3 Mean =
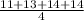 = 13
= 13
Sample 4 Mean =
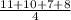 = 9
= 9
Sample 5 Mean =
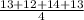 = 13
= 13
Now, add all the means and find out the mean of the sample size.
Mean of the sample size =
 =
=
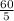 = 12
= 12
Secondly, we have to find out the maximum and minimum of the observations in each sample.
Sample 1 (max, min) = (14,10)
Sample 2 (max, min) = (16,11)
Sample 3 (max, min) = (14,11)
Sample 4 (max, min) = (11,7)
Sample 5 (max, min) = (14,12)
Thirdly, we need to calculate the Range of each sample.
Range = Max - Min
Range 1 = 14-10 = 4
Range 2 = 16-11 = 5
Range 3 = 14-11 = 3
Range 4 = 11-7 = 4
Range 5 = 14-12 = 2
ΣRange = 18
Now, sum all the ranges and divide it by the number of samples n.
(Range-bar) = ΣRange/n
Range-bar = 18/5
Range-bar = 3.6
Now, we need value of A2 for the sample size of 4. So, it can find out from the table of control chart constants which is attached for your reference.
A2 = 0.729
Now, we have all the data required to calculate the UCL.
UCL = (Mean of the sample size) + (A2 * Range-bar)
UCL = (5) + (0.729x 3.6)
UCL = 14.624