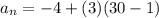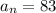Question

What is the 30th term of the linear sequence below?
-4, -1,2,5,8,...

Answer 1

The 30th term is 83

Explanation:

we know that

An arithmetic sequence is a sequence of numbers such that the difference of any two successive members of the sequence is a constant called the common difference d

in this problem

`a_1=-4\\a_2=-1\\a_3=2\\a_4=5\\a_5=8`

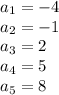
so

`a_2-a_1=-1-(-4)=3\\a_3-a_2=-2-(-1)=3\\a_4-a_3=-5-2=3\\a_5-a_4=-8-5=3`

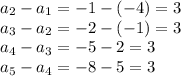
The common difference d is 3

We can write an Arithmetic Sequence as a rule:

`a_n=a_1+d(n-1)`

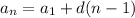
Find out the 30th term

we have

`n=30\\d=3\\a_1=-4`

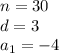
substitute

`a_n=-4+(3)(30-1)`

`a_n=-4+(3)(29)`

`a_n=83`