Answer:
The distance between R and R' is 3 units ⇒ 1st answer
Explanation:
A dilation is a transformation that produces an image that is the same
shape as the original, but in a different size.
If the image is larger than the original figure then dilation is called an
enlargement.
If the image is smaller than the original figure then the dilation
is called a reduction.
The image of a line by dilation parallel to the original line if the original
line not passes through the center of dilation.
Line segment QR is dilated to create line segment Q'R'
∴ QR is parallel to Q'R'
The factor of dilation is 1.5
∴ The length of Q'R' is 1.5 the length of QR
In Δs TRQ and TR'Q'
∵ QR // Q'R'
∴ m∠TRQ = m∠TR'Q'
∴ m∠TQR = m∠TQ'R'
∵ ∠T is common in the two triangles
∴ ΔTRQ is similar to ΔTR'Q'
∴
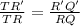
∵
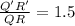
∵ TR' = TR + y
∵ Tr = 6 units
∴ TR' = 6 + y units
∵
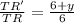
∴
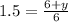
Multiply both sides by 6
∴ 9 = 6 + y
Subtract 6 from both sides
∴ 3 = y
* The distance between R and R' is 3 units