Question

PLZ HELP Describe the end behavior and determine whether the graph represents an odd-degree or an even-degree polynomial function. Then state the number of real zeros. simple answer

Answer 1

x=8

Explanation:

6. an odd-degree polynomial function.

f(x)⇒-∞ as x⇒-∞ and f(x)⇒∞ as x⇒∞

Step by step explanation;

6. The graph represent an odd-degree polynomial function.

The graph enters the graphing box from the bottom and goes up leaving through the top of the graphing box.This is a positive polynomial whose limiting behavior is given by;

f(x)⇒-∞ as x⇒-∞ and f(x)⇒∞ as x⇒∞

Answer 2

End behavior:
`f(x)\rightarrow -\infty\text{ as }x\rightarrow -\infty` and
`f(x)\rightarrow \infty\text{ as }x\rightarrow \infty`

The function has odd-degree.

The number of real zeros in 5.

Explanation:

From the given graph it is clear that the graph approaches towards negative infinite as x approaches towards negative infinite.

`f(x)\rightarrow -\infty\text{ as }x\rightarrow -\infty`

The graph approaches towards positive infinite as x approaches towards positive infinite.

`f(x)\rightarrow \infty\text{ as }x\rightarrow \infty`

For even-degree the polynomial has same end behavior.

For odd-degree the polynomial has different end behavior.

Since the given functions has different end behavior, therefore the graph represents an odd-degree polynomial function.

If the graph of a function intersects the x-axis at a point then it is a zero of the function.

If the graph of a function touch the x-axis at a point and return then it is a zero of the function with multiplicity 2. It means, the function has 2 equal zeros.

The graph intersect the x -axis at 3 points and it touch the x-axis at origin. So, the number of zeros is

`N=3+2=5`

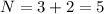
The number of real zeros is 5.