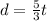Answer:
Option B. d = 5/3t
Explanation:
see the attached figure to better understand the problem
we know that
A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
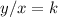 or
or

In a proportional relationship the constant of proportionality k is equal to the slope m of the line and the line passes through the origin
Let
d -----> the distance in meters
t ----> the time in seconds
Looking at the graph we have the point (3,5)
That means ----> For t=3 sec, d=5 m
Find the value of k
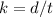
substitute the value of y and the value of x

The linear equation is

substitute the value of k