Question

Evaluate M^2 /p^2 for M = 10, N =-5p and P = -2

Answer 1

The solution of
`\bold{(M^(2))/(P^(2))}` for M = 10, N = -5P and P = -2 is 25

Solution:

From question, given that the value of M is 10 and N is -5p and P is -2

We have to evaluate the value of
`(M^(2))/(P^(2))`,

By substituting the values of M and N, we get

`(M^(2))/(P^(2)) = (10^(2))/((-2)^(2))`

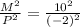
Expanding
`\bold{10^(2)}`:

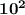Here 10 is the base value and 2 is the exponent value. So the base term 10 is multiplied by itself two times.

`10^(2) = 10 * 10 = 100`

Similarly expanding
`\bold{(-2)^(2)}`:

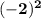Here -2 is the base term and 2 is the exponent value. So the base term -2 is multiplied by itself two times.

`(-2)^(2) = -2 * -2 = 4`

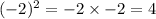
So the equation
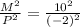`(M^(2))/(P^(2)) = (10^(2))/((-2)^(2))` becomes,

`(M^(2))/(P^(2)) = (100)/(4)`

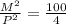
By dividing 100 by 4 , we get the result as 25

Hence the solution of
`\bold{(M^(2))/(P^(2))}` when M = 10 and P = -2 is 25