Let f and s be the ages of the father and the son. We have
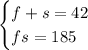
From the first equation we derive
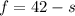
Substitute this expression for f in the second equation and we have
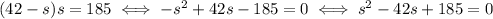
The solutions to this equation are s=5 or s=37
Since the sum of the ages must be 42, the solutions would imply

We can only accept the first solution, since the second would imply a son older than his father!