Question

A lead ball is dropped 30 feet from a church tower. If the acceleration due to gravity is 9.8m s^-2, how long does it take the ball to fall to the ground?

Answer 1

final velocity of a falling object = 0

and acceleration of a falling object is negative

now using the expression ( Newton's 3rd equation of motion)

`{v}^(2) = {u}^(2) - 2gs`

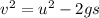
where the parameters have their usual meaning

making

`{u}^(2) \: the \: subject`

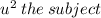
thus

`{u}^(2) = 2gs`

`u = √(2gs)`

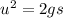
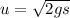
from the question,

g= 9.8m/s^2

s = 30m

substitute them into the equation

`u = √(2(9.8 * 30))`

`u = √(588)`

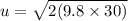
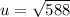
u = 24.25m/s

but the question is demanding for time but not the initial velocity

so substitute them in the

Newton's first equation of motion

where

V = u - gt

but from the question,

v= 0 and the acceleration is negative because it's a free fall

substitute the values into the equation

0 = 24.24 -9.8t

making t the subject

9.8t = 22.24

dividing through by 9.8

9.8t/9.8 = 22.24/9.8

t = 2.3s . therefore, it would take 2.3s for the ball to hit the ground.