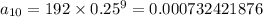Answer:
The sequence shown is geometric
Recursive function:
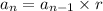
with
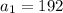
Explicit function:
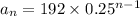
10th term: 0.000732421876
Explanation:
In a geometric sequence the n+1 term divide by the n term is constant
48/192 = 0.25
12/48 = 0.25
3/12 = 0.25
From this result we can deduce the recursive function:
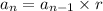
with
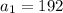
Explicit function:
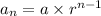
where a is the first term in the sequence (= 192) and r is the common ratio (= 0.25). Replacing:
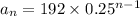
The 10th term is: