Question

What is the angular diameter in arc seconds of a star like the sun (diameter= 1,400,000 km) located 8 light years (7.57 x 10^13 km) fom earth?

a. 0.038

b. 8

c. 0.0038

d.200,00

e. 1,400,000

Answer 1

Option (C)

Step-by-step explanation:

Here, Diameter= 1,400,000 km = 1.4 x 10^6 km

Distance= 7.57 x 10^13 km

According to the formula, angular diameter= Diameter/Distance

`\alpha = (Diameter)/(Distance)`

`=(1.4* 10^6)/(7.57)* 10^(-13)`

`=0.18* 10^(-7)\text{ radian}`

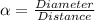
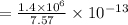
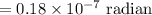
Since 1 radian=206265 arc second,

Therefore,

`206265* 0.18* 10^(-7)`

`=(37127.7)/(10^7)`

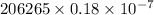
= .00371 arc second

Hence, the approximate answer is option (C) i.e. 0.0038 arc second.

Answer 2

`\theta = 0.0038\ arc\ sec`

option c

Step-by-step explanation:

given data:

Diameter of a star = 1,400,000 km

star distance from sun
`= 7.57* 10^(13) km`

we know that

Angle is given as

`\theta = (d)/(r) = (14* 10^5)/(7.57* 10^(13))`

`\theta = 1.849* 10^(-8) rad`

we know that

`1\ arc\ second  = 4.84* 10^(-6) rad`

`1 rad = (1\ arc\ sec)/(4.84* 10^(-6))`

SO,
`\theta = (1.849*10^(-8))/(4.84*10^(-6))`

`\theta = 3.82\time 10^(-3) arc sec`

`\theta = 0.0038\ arc\ sec`

option c