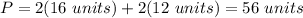2 Answers

Anil Kothari · Answer 1 · 2020-09-05T05:57:21+0000

Answer: Third option.

Step-by-step explanation:

The missing figure is attached.

The perimeter of a rectangle can be calculated with:

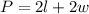
P=2l+2w

Where "l" is the length and "w" is the width.

We can see that the width of this rectangle is:

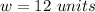
$w=12\ units$

So, we need to find the lenght.

Let be P the point of intersection of the diagonals.

The diagonals of a rectangle are equal.

Since:

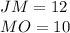
$JM=12\\MO=10$

We know that, by definition:

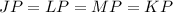
JP=LP=MP=KP

Then, we can find the lenght of the rectangle by using the Pythagorean Theorem:

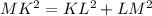
MK^2=KL^2+LM^2

We can identify that:

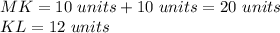
$MK=10\ units+10\ units=20\ units\\KL=12\ units$

Then, subsituting values and solving for "LM", we get:

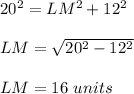
$20^2=LM^2+12^2\\\\LM=√(20^2-12^2)\\\\LM=16\ units$

Substituting values into the formula for calculate the perimeter, we get:

$P=2(16}\ units)+2(12\ units)=56\ units$

Please log in or register to add a comment.