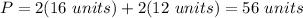Answer: Third option.
Step-by-step explanation:
The missing figure is attached.
The perimeter of a rectangle can be calculated with:
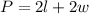
Where "l" is the length and "w" is the width.
We can see that the width of this rectangle is:
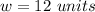
So, we need to find the lenght.
Let be P the point of intersection of the diagonals.
The diagonals of a rectangle are equal.
Since:
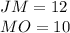
We know that, by definition:
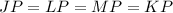
Then, we can find the lenght of the rectangle by using the Pythagorean Theorem:
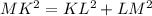
We can identify that:
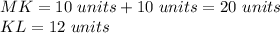
Then, subsituting values and solving for "LM", we get:

Substituting values into the formula for calculate the perimeter, we get: