Question

A model airplane is flying horizontally due north at 44 ​mi/hr when it encounters a horizontal crosswind blowing east at 44 ​mi/hr and a downdraft blowing vertically downward at 22 ​mi/hr. a. Find the position vector that represents the velocity of the plane relative to the ground. b. Find the speed of the plane relative to the ground.

Answer 1

Step-by-step explanation:

Let i, j and k represents east, north and upward direction respectively.

Velocity due north,
`v_a=44j\ mi/hr`

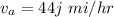
Velocity of the crosswind,
`v_w=44i\ mi/hr`

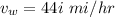
Velocity of downdraft,
`v_d=-22k\ mi/hr` (downward direction)

(a) Let v is the position vector that represents the velocity of the plane relative to the ground. It is given by :

`v=44i+44j-22k`

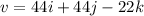
(b) The speed of the plane relative to the ground can be calculated as :

`v=√(44^2+44^2+22^2)`

v = 66 m/s

Hence, this is the required solution.