Question

A steel rotating-beam test specimen has an ultimate strength Sut of 1600 MPa. Estimate the life (N) of the specimen if it is tested at a completely reversed stress amplitude σa, of 900 MPa.

Answer 1

the life (N) of the specimen is 46400 cycles

Step-by-step explanation:

given data

ultimate strength Su = 1600 MPa

stress amplitude σa = 900 MPa

to find out

life (N) of the specimen

solution

we first calculate the endurance limit of specimen Se i.e

Se = 0.5× Su .............1

Se = 0.5 × 1600

Se = 800 Mpa

and we know

Se for steel is 700 Mpa for Su ≥ 1400 Mpa

so we take endurance limit Se is = 700 Mpa

and strength of friction f = 0.77 for 232 ksi

because for Se 0.5 Su at
`10^(6)` cycle = (1600 × 0.145 ksi ) = 232

so here coefficient value (a) will be

a =
`((f*Su)^2)/(Se)`

a =
`((0.77*1600)^2)/(700)`

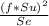
a = 2168.3 Mpa

so

coefficient value (b) will be

a = -
`(1)/(3)`log
`((f*Su))/(Se)`

b = -
`(1)/(3)`log
`((0.77*1600))/(700)`

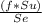
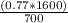
b = -0.0818

so no of cycle N is

N =
`(( \sigma a)/(a))^(1/b)`

put here value

N =
`(( 900)/(2168.3))^(1/-0.0818)`

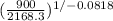
N = 46400

the life (N) of the specimen is 46400 cycles