Question

Two fluid layers with different viscosities ( u1= 0.1 Pa ∙ s and u2 = 0.2 Pa ∙ s) are sandwiched between two plates of area A = 1 m2. Each layer is h = 1 mm thick. Find the force F necessary to make the upper plate move at a speed U = 1 m/s. Also, find the fluid velocity at the interface between the two fluids.

Answer 1

Step-by-step explanation:

The given data is as follows.

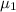`\mu_(1)` = 0.1 Pa.s,
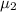`\mu_(2)` = 0.2 Pa.s

`h_(1)` =
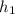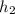`h_(2)` = 1 mm =
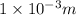`1 * 10^(-3) m` (as 1 m = 1000 mm)

As the velocity gradients are linear so, the shear stress will be the same throughout.

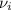`\\u_(i)` = velocity at the interface

`\tau = \mu_(1) (d\mu_(1))/(dy_(1)) = \mu_(2) (d\mu_(2))/(dy_(2))`

`\mu_(1) * (\\u_(i))/(h_(1)) = \mu_(2) * (\\u - \\u_(i))/(h_(2))`

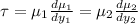
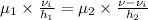
or,
`\\u_(i) = (\\u)/(1 + (\mu_(1)h_(2))/(\mu_(2)h_(1)))`

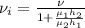
Now, putting the given values into the above formula as follows.

`\\u_(i) = (\\u)/(1 + (\mu_(1)h_(2))/(\mu_(2)h_(1)))`

=
`(1 m/s)/(1 + (0.1 * 1)/(0.2 * 1))`

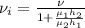
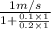
= 0.667 m/s

Hence, force required will be F =
`\tau * Area`

or, F =
`\mu_(1) * (\\u_(i))/(h_(1)) * Area`

=
`0.1 * (0.667)/(0.001) * 1`

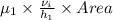
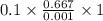
= 66.67 N

Thus, we can conclude that the fluid velocity is 0.667 m/s and force necessary to make the upper plate move at a speed U = 1 m/s is 66.67 N.