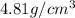Question

Titanium has an HCP unit cell for which the ratio of the lattice parameters cais 1.58. If the radius of the Be atom is 0.1445 nm, (a) determine the unit cell volume, and (b) calculate the theoretical density of Ti, given that its atomic weight is 47.87 g/mol

Answer 1

(a) The volume of unit cell is,
`9.91* 10^(-23)cm^3/\text{ unit cell}`

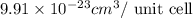
(b) The theoretical density of Ti is,
`4.81g/cm^3`

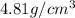
Explanation :

(a) First we have to calculate the volume of the unit cell.

Formula used :

`V=6r^2c\sqrt {3}`

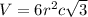
where,

V = volume of unit cell = ?

r = atomic radius =
`0.1445nm=1.445* 10^(-8)cm`

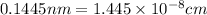
conversion used :
`(1nm=10^(-7)cm)`

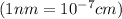
Ratio of lattice parameter = c : a = 1.58 : 1

So, c = 1.58 a

And, a = 2r

c = 1.58 × 2r

Now put all the given values in this formula, we get:

`V=6* r^2* (1.58* 2r)\sqrt {3}`

`V=6* r^3* (1.58* 2)\sqrt {3}`

`V=6* (1.445* 10^(-8)cm)^3* (1.58* 2)\sqrt {3}`

`V=9.91* 10^(-23)cm^3/\text{ unit cell}`

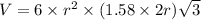
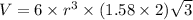
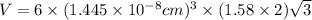
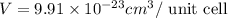
The volume of unit cell is,
`9.91* 10^(-23)cm^3/\text{ unit cell}`

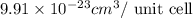
(b) Now we have to calculate the density of Ti.

Formula used for density :

`\rho=(Z* M)/(N_(A)* a^(3))`

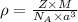
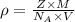`\rho=(Z* M)/(N_(A)* V)` ..........(1)

where,

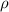`\rho` = density of Ti = ?

Z = number of atom in unit cell = 6 atoms/unit cell (for HCP)

M = atomic mass = 47.87 g/mol

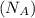`(N_(A))` = Avogadro's number =
`6.022* 10^(23)atoms/mole`

`a^3=V` = volume of unit cell =
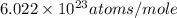
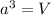`9.91* 10^(-23)cm^3/\text{ unit cell}`

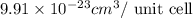
Now put all the values in above formula (1), we get:

`\rho=(6* 47.87)/((6.022* 10^(23))* (9.91* 10^(-23)))`

`\rho=4.81g/cm^3`

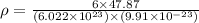
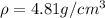
The theoretical density of Ti is,
`4.81g/cm^3`