Question

Pressure gauge at the top of a vertical oil well registers 140 bars. The oil well is 6000 m deep and filled with natural gas down to a depth of 4700 m and filled with oil (density=700 kg/m3) the rest of the way to the bottom of the well at 15°C. The compressibility factor Z=0.80 for natural gas and its molecular weight is 18.9.

Determine the pressure at (a) the natural gas-oil interface and at (b) the bottom of the well at 15°C.

Answer 1

Step-by-step explanation:

(a) The given data is as follows.

Pressure on top (
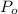`P_(o)`) = 140 bar =
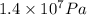`1.4 * 10^(7) Pa` (as 1 bar =
`10^(5)`)

Temperature =
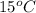`15^(o)C` = (15 + 273) K = 288 K

Density of gas =
`(PM)/(ZRT)`

`(dP)/(dZ) = \rho * g`

`(dP)/(dZ) = \int (PM)/(ZRT)`

`\int_{P_(o)}^{P_(1)} (dP)/(dZ) = (Mg)/(ZRT) \int_(0)^(4700) dZ`

`ln ((P_(1))/(P_(o))) = (18.9 * 10^(-3) * 9.81 * 4700 m)/(0.80 * 8.314 J/mol K * 288 K)`

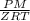
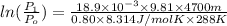
= 0.4548

`P_(1) = P_(o) * e^(0.4548)`

=
`1.4 * 10^(7) Pa * 1.5797`

=
`2.206 * 10^(7) Pa`

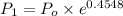
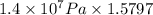
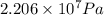
Hence, pressure at the natural gas-oil interface is
`2.206 * 10^(7) Pa`.

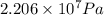(b) At the bottom of the tank,

`P_(2) = P_(1)  + \rho * g * h`

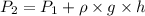
= 2.206 \times 10^{7} Pa + 700 \times 9.81 \times (6000 - 4700)[/tex]

=
`309.8 * 10^(5) Pa`

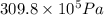
= 309.8 bar

Hence, at the bottom of the well at
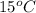`15^(o)C` pressure is 309.8 bar.