Answer: The amount of sample left after 58.2 years is 3.96 grams and after 291 years is 0.015 grams
Step-by-step explanation:
All the radioactive reactions follows first order kinetics.
The equation used to calculate half life for first order kinetics:
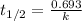
We are given:
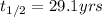
Putting values in above equation, we get:

Rate law expression for first order kinetics is given by the equation:
 ......(1)
......(1)
k = rate constant
t = time taken for decay process
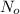 = initial amount of the reactant
= initial amount of the reactant
N = amount left after decay process
We are given:
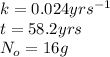
Putting values in equation 1, we get:
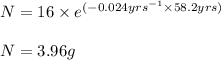
We are given:

Putting values in equation 1, we get:
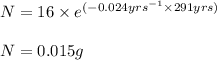
Hence, the amount of sample left after 58.2 years is 3.96 grams and after 291 years is 0.015 grams