Answer:
The value of r is 9
Explanation:
- The slope of a line whose endpoints are
 and
and
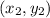 is
is
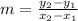
- A line passes through points (6 , r) and (3 , 3)
- The slope of the line is m = 3
- We need to find the value of r
- Let
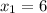 and
and
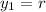
- Let
 and
and
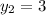
∵ m = 2
- Substitute these values in the rule of the slope
∴
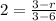
∴
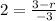
- Multiply both sides by -3
∴ - 6 = 3 - r
- Add r to both sides
∴ r - 6 = 3
- Add 6 to both sides
∴ r = 9
* The value of r is 9