Answer :
(a) The change in internal energy of the gas is 22.86 kJ.
(b) The change in enthalpy of the gas is 34.29 kJ.
Explanation :
(a) The formula used for change in internal energy of the gas is:
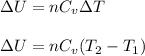
where,
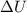 = change in internal energy = ?
= change in internal energy = ?
n = number of moles of gas = 5 moles
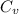 = heat capacity at constant volume = 2R
= heat capacity at constant volume = 2R
R = gas constant = 8.314 J/mole.K
 = initial temperature =
= initial temperature =
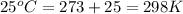
 = final temperature =
= final temperature =

Now put all the given values in the above formula, we get:
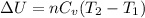
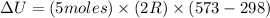

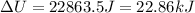
The change in internal energy of the gas is 22.86 kJ.
(b) The formula used for change in enthalpy of the gas is:
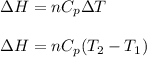
where,
 = change in enthalpy = ?
= change in enthalpy = ?
n = number of moles of gas = 5 moles
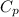 = heat capacity at constant pressure = 3R
= heat capacity at constant pressure = 3R
R = gas constant = 8.314 J/mole.K
 = initial temperature =
= initial temperature =
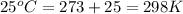
 = final temperature =
= final temperature =

Now put all the given values in the above formula, we get:
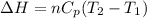
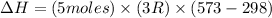
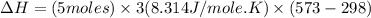
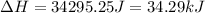
The change in enthalpy of the gas is 34.29 kJ.