Question

A slab of dry wood of 4-in thickness and sealed edges is exposed to air of 40% relative humidity. Assuming that the two unsealed surfaces of the wood immediately jump to an equilibrium moisture content of 8 lb H2O per 100 lb of dry wood, determine the time for the moisture content at the center of the slab to reach 1% of the equilibrium value using the semi-infinite slab solution. Assume a diffusivity of water of 6.00e-006 cm2/s.

Answer 1

Step-by-step explanation:

It is given here that a slab is made up of dry wood.

Thickness of slab = 4 inch

It is given condition that the edges of the slab are sealed and exposed to air.

Given the relative humidity of air = 40%

The surface of slab is unsealed and reached to the equilibrium moisture content =
`(8 lb H_(2)O)/(100 lb dry wood)`.

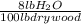Given, the diffusivity of water in the slab =
`6 * 10^(-6) cm^(2)/s`.

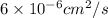As per the given condition 1% moisture content will be taken by multiplying the moisture content by 1%, i.e. 0.01.

It is given that the thickness of slab is in inch, so converting the thickness of slab in cm as follows.

Thickness of slab =
`4 inch * 2.54 inch/cm`

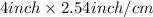
= 10.16 cm (As, 1 inch = 2.54 cm)

Since, the equilibrium moisture content is required to calculate at the center of the slab.

The center of the slab, from the semi-infinite slab solution will be taken from thickness t = 0.

The thickness at center = 10.16 cm

Hence, calculate total thickness at the center of slab as follows.

`\frac{\text{total thickness of slab}}{2}`

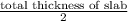
= 5.08 cm

Now, by semi-infinite solution, and by 40% relative humidity of air, time for moisture content to reach at the center of the slab, to 1% of its equilibrium value will be calculated as follows.

Time(Seconds) =
`\frac{thickness^(2)(cm^(2)) * \text{relative humidity} * 0.01 * \text{equilibrium content} * \text{equilibrium moisture}}{\text{diffusivity(cm/s)}}`

Time (sec) =
`\frac{5.08 cm * 5.08 cm * 0.4 * \text{relative humidity} * 0.01 \text{equilibrium content} * 8 lb H_(2)O}{100 lb dry.wood * 6 * 10{-6} cm^(2)/s \text{diffusivity}}`

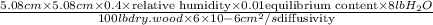
Time (Seconds) = 1376.34 seconds

Thus, we can conclude that the time required for the moisture content at the center of the slab to reach to 1 % of equilibrium value is 1376.34 seconds.