Question

A water treatment plant has a total flow of 45 MGD (mega gallons per day). The plant was designed with five sedimentation basins, each with a total volume of 2500 m3.

Originally, the plant was operating the basins in series: the entire flow goes through one tank, then the second, and so on. What is the retention time in each tank?

The engineer realizes that the sedimentation would improve if they changed the operation to parallel flow. Under this new configuration, the flow is evenly split between the four tanks. What is the retention time in each tank?

Answer 1

a) 21.133 minutes for series

b) 84.54 minutes when split into 4

Step-by-step explanation:

Data provided:

Total flow, V₀ = 45 MGD

total volume of each basin, V = 2500 m³

Now,

1 MGD = 3785.4118 m³/day

also,

1 day = 1440 minutes

thus,

45 MGD = 45 × 3785.4118 m³/day

or

45 MGD = 170343.5305 m³/day

and,

170343.5305 m³/day in 'm³/min'

= 170343.5305 / 1440

= 118.2941 m³/min.

Therefore,

The retention time, t =
`\frac{\textup{Volume of tank}}{\textup{Volumetric Flowrate }}`

or

The retention time, t =
`\frac{\textup{2500}}{\textup{118.2941 }}`

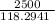
or

The retention time, t = 21.13 min

Hence,

for series of tanks the retention time is 21.133 min.

Now,

on splitting the tanks in 4

the volumetric flow rate will be

=
`\frac{\textup{118.2941}}{\textup{4}}`

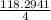
= 29.57 m³/min.

Therefore,

The retention time =
`\frac{\textup{Total Volume of tank}}{\textup{Volumetric Flowrate }}`

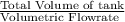
or

The retention time, t =
`\frac{\textup{2500}}{\textup{29.57 }}`

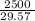
or

The retention time, t = 84.54 min