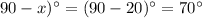Answer:
The measure of the complement of angle A is
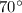
Step-by-step explanation:
we know that
If two angles are complementary, then their sum is equal to 90 degrees
If two angles are supplementary, then their sum is equal to 180 degrees
Let
x ----> the measure of angle A
(90-x) ----> the measure of the complement of angle A
(180-x) ---> the measure of the supplement of angle A
we know that
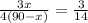 -----> equation A
-----> equation A
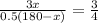 ----> equation B
----> equation B
Solve equation A or equation B to determine the value of x
Solve equation A
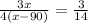
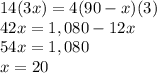
Verify the value of x in the equation B
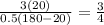
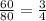
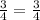 ---> is ok
---> is ok
Find out the measure of the complement of angle A
(