Answer:
A)Boiling point constant of benzene = 2.63°C/m
B) 242.77 g/mol is the molar mass of the solute.
Step-by-step explanation:

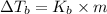
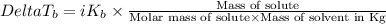
where,
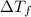 =Elevation in boiling point
=Elevation in boiling point
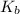 = boiling point constant od solvent= 3.63 °C/m
= boiling point constant od solvent= 3.63 °C/m
1 - van't Hoff factor
m = molality
A) Mas of solvent = 500 g = 0.500 kg
T = 80.1°C ,
 =82.73°C
=82.73°C

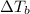 = 82.73°C - 80.1°C = 2.63°C
= 82.73°C - 80.1°C = 2.63°C

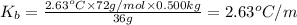
Boiling point constant of benzene = 2.63°C/m
B) Mass of solute = 1.2 g
Molar mas of solute = M
Mass of solvent = 50 g= 0.050 kg
i = 1
T = 80.1°C ,
 =80.36°C
=80.36°C
 =80.36°C - 80.1°C = 0.26°C
=80.36°C - 80.1°C = 0.26°C
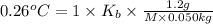
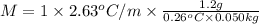
M = 242.77 g/mol
242.77 g/mol is the molar mass of the solute.