Question

Consider the relationship (y+3)2 = b/(x-2), where y and x are variables and bis a constant. On rectangular coordinate paper, what is the slope of a graph of In(y+3) on the vertical axis versus In(x-2) on the horizontal axis?

Answer 1

(-1) is the slope of a graph of In(y+3) on the vertical axis versus In(x-2) on the horizontal axis.

Step-by-step explanation:

`((y+3))/(2) = (b)/((x-2))`

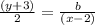
Taking natural logarithm on both the sides:

`\ln [(y+3)]-\ln[2]=\ln [b]-\ln [(x-2)]`

`\ln [(y+3)]=\ln[2]+\ln [b]-\ln [(x-2)]`

`\ln [(y+3)]=\ln {[2* b]-\ln [(x-2)]`

Slope intercept form is generally given as:

`y=mx+c`

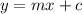
m = slope, c = intercept on y axis or vertical axis

On rearranging equation:

`\ln [(y+3)]=(-1)* \ln [(x-2)]+\ln {2b}`

y = ln [(y+3)], x = ln [(x-2)], m=-1 , c = ln 2b

(-1) is the slope of a graph of In(y+3) on the vertical axis versus In(x-2) on the horizontal axis.