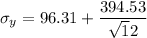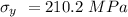Question

An alloy with an average grain diameter of 35 μm has a yield strength of 163 Mpa, and when it undergoes strain hardening, the grain diameter reduces to 17 μm with an increase in yield strength to 192 MPa. If the coarseness of the alloy desired for a particular application cannot exceed 12 μm, what will be the expected yield strength?

Answer 1

`\sigma_y\ =210.2\ MPa`

Step-by-step explanation:

Given that

d= 35 μm ,yield strength = 163 MPa

d= 17 μm ,yield strength = 192 MPa

As we know that relationship between diameter and yield strength

`\sigma_y=\sigma_o+(K)/(\sqrt d)`

`\sigma_y\ =Yield\ strength`

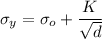
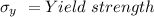
d = diameter

K =Constant

`\sigma_o\ =material\ constant`

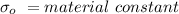
So now by putting the values

d= 35 μm ,yield strength = 163 MPa

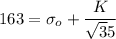`163=\sigma_o+(K)/(\sqrt 35)` ------------1

d= 17 μm ,yield strength = 192 MPa

`192=\sigma_o+(K)/(\sqrt 17)` ------------2

From equation 1 and 2

`192-163=(K)/(\sqrt 17)-(K)/(\sqrt 35)`

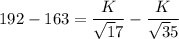
K=394.53

By putting the values of K in equation 1

`163=\sigma_o+(394.53)/(\sqrt 35)`

`\sigma_o\ =96.31\ MPa`

`\sigma_y=96.31+(394.53)/(\sqrt d)`

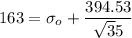
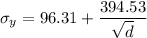
Now when d= 12 μm

`\sigma_y=96.31+(394.53)/(\sqrt 12)`

`\sigma_y\ =210.2\ MPa`