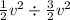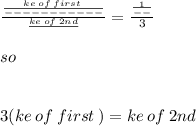Question

One object has a mass of 1 kg and another object has a mass of 3 kg. If the speeds are the same, which of the following is true about their kinetic energy?

Their masses are the same.
The object with a higher mass has three times the kinetic energy of the less massive object.
It is impossible to determine without the speeds.
The object with a smaller mass has a greater kinetic energy than the object with a higher mass.

Answer 1

The object with a higher mass has three times the kinetic energy of the less massive object.

We know that K.E.= 1/2 mv²

mass of first object = 1kg

speed = v

So K.E. = 1/2mv²

= 1/2 × (1) × v²

=

`\: \: \: \: \: \: \: \: \: = (1)/(2) {v}^(2) \\`

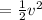
Now the mass of second body = 3kg

speed = v

So K.E. = 1(3)v²/2

=

`\: \: \: \: \: \: \: \: \: = \: \: (3)/(2) {v}^(2) \\`

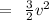
now

K.E of first / KE of 2nd

`(1)/(2) {v}^(2) / (3)/(2) {v}^(2) \\`

`\frac{ (ke \: of \: first \: )/( - - - - - - - - - - -) }{ \frac{ke \: of \: 2nd}{} } = ( (1)/( - -) )/( 3 ) \\ \\ so \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \\ \\ \\ 3(ke \: of \: first \:) = ke \: of \: 2nd`