Question

Jack has 63 pennies, dimes, and quarters worth $6.30. If the number of dimes is three less than the number of quarters, how many of each coin does he have? Three variable application

Answer 1

18 quarters

30 pennies

15 dimes

Explanation:

Let number of quarters be q, number of pennies be p, number of dimes be d

The value of pennies is 0.01, the value of quarters is 0.25 and value of dimes is 0.10.

Jack has 63 pennies, dimes, and quarters worth $6.30:

We can write:

p + q + d = 63

0.01p + 0.25q + 0.10d = 6.30

Also, the number of dimes is three less than the number of quarters:

We can write:

d = q - 3

Now we have written 3 equations. Replacing 3rd equation in 1st gives us:

p + q + (q-3) = 63

p + 2q -3 = 63

p + 2q = 66

Solving for p:

p = 66 - 2q

Now we can use this and the 3rd equation and replace p and d with q:

0.01p + 0.25q + 0.10d = 6.30

0.01(66-2q) + 0.25q + 0.10(q-3) = 6.30

Solving for q, gives us:

`0.01(66-2q) + 0.25q + 0.10(q-3) = 6.30\\0.66-0.02q+0.25q+0.10q-0.3=6.30\\0.36+0.33q=6.30\\0.33q=5.94\\q=18`

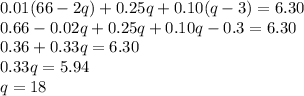
There are 18 quarters

Since, p = 66 - 2q, there are:

p = 66 - 2 (18) = 30 pennies

Also,

d = q - 3, so d = 18 - 3 = 15 dimes

Hence, there are:

18 quarters

30 pennies

15 dimes