Answer:
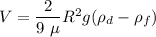
Step-by-step explanation:
Given that
Radius =R
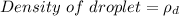
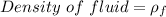
When drop let will move downward then so
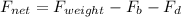
Fb = Bouncy force
Fd = Drag force
We know that
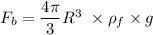
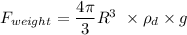
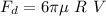
μ=Dynamic viscosity of fluid
V= Terminal velocity
So at the equilibrium condition
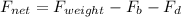
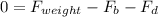
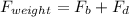
So
This is the terminal velocity of droplet.