Question

Five million gallons per day (MGD) of wastewater, with a concentration of 10.0 mg/L of a conservative pollutant, is released into a stream having an upstream flow of 10 MGD and pollutant concentration of 3.0 mg/L. (a) What is the concentration in ppm just downstream? (b) How many pounds of substance per day pass a given spot downstream? (You may want the conversions 3.785 L/gal and 2.2 kg/lbm from Appendix A.)

Answer 1

To find the concentration in ppm just downstream, we calculate the mass of the pollutant using the flow rate and concentration. The concentration in ppm just downstream is 50 ppm. To find the number of pounds of substance per day passing a given spot downstream, we convert the mass from grams to pounds.

Step-by-step explanation:

In order to find the concentration in ppm just downstream, we need to calculate the mass of pollutant that is being released into the stream. We can use the following formula:

Mass = Flow rate x Concentration

Using the given flow rates and concentrations:

Upstream Mass = 10 MGD x 3.0 mg/L = 30 mg/L

Downstream Mass = 5 MGD x 10.0 mg/L = 50 mg/L

So the concentration in ppm just downstream is:

50 mg/L x (1 ppm/1 mg/L) = 50 ppm

To find the number of pounds of substance per day passing a given spot downstream, we will need to calculate the mass in pounds. We can use the following conversions:

1 lbm = 2.2 kg

1 kg = 1000 g

1 g = 1000 mg

Using the given flow rate and concentration:

Downstream Mass (in g/day) = 5 MGD x 10.0 mg/L = 50,000 g/day

Downstream Mass (in kg/day) = 50,000 g/day x (1 kg/1000 g) = 50 kg/day

Downstream Mass (in lbm/day) = 50 kg/day x (1 lbm/2.2 kg) = 22.7 lbm/day

So the number of pounds of substance per day passing a given spot downstream is approximately 22.7 pounds.

Answer 2

a) The concentration in ppm (mg/L) is 5.3 downstream the release point.

b) Per day pass 137.6 pounds of pollutant.

Step-by-step explanation:

The first step is to convert Million Gallons per Day (MGD) to Liters per day (L/d). In that sense, it is possible to calculate with data given previously in the problem.

Million Gallons per day
`1 MGD = 3785411.8 litre/day = 3785411.8 L/d`

`F_1 = 5 MGD ((3785411.8 L/d)/(1MGD) ) = 18927059 L/d\\F_2 =10 MGD ((3785411.8 L/d)/(1MGD) )= 37854118 L/d`

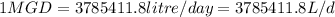
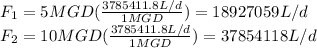
We have one flow of wastewater released into a stream.

First flow is F1 =5 MGD with a concentration of C1 =10.0 mg/L.

Second flow is F2 =10 MGD with a concentration of C2 =3.0 mg/L.

After both of them are mixed, the final concentration will be between 3.0 and 10.0 mg/L. To calculate the final concentration, we can calculate the mass of pollutant in total, adding first and Second flow pollutant, and dividing in total flow. Total flow is the sum of first and second flow. It is shown in the following expression:

`C_f = (F1*C1 +F2*C2)/(F1 +F2)`

Replacing every value in L/d and mg/L

`C_f = (18927059 L/d*10.0 mg/L +37854118 L/d*10.0 mg/L)/(18927059 L/d +37854118 L/d)\\C_f = (302832944 mg/d)/(56781177 L/d) \\C_f = 5.3 mg/L`

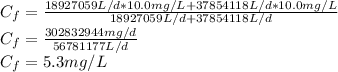
a) So, the concentration just downstream of the release point will be 5.3 mg/L it means 5.3 ppm.

Finally, we have to calculate the pounds of substance per day (Mp).

We have the total flow F3 = F1 + F2 and the final concentration
`C_f`. It is required to calculate per day, let's take a time of t = 1 day.

`F3 = F2 +F1 = 56781177 L/d \\M_p = F3 * t * C_f\\M_p = 56781177 (L)/(d) * 1 d * 5.3 (mg)/(L)\\M_p = 302832944 mg`

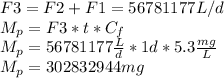
After that, mg are converted to pounds.

`M_p = 302832944 mg ((1g)/(1000 mg) ) ((1Kg)/(1000 g) ) ((2.2 lb)/(1 Kg) )\\M_p = 137.6 lb`

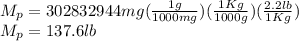
b) A total of 137.6 pounds pass a given spot downstream per day.