Question

Water enters a 4.00-m3 tank at a rate of 6.33 kg/s and is withdrawn at a rate of 3.25 kg/s. The tank is initially half full.

How long does it take for the tank to overflow?

Answer 1

Step-by-step explanation:

The given data is as follows.

Volume of tank = 4
`m^(3)`

Density of water = 1000
`kg/m^(3)`

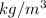
Since, the tank is initially half-filled. Hence, the volume of water in the tank is calculated as follows.

`(1)/(2) * 4 = 2 m^(3)`

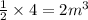
Also, density of a substance is equal to its mass divided by its volume. Therefore, initially mass of water in the tank is as follows.

Mass =
`Density * initial volume`

=
`1000 * 2`

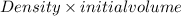
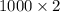
= 2000 kg

Whereas mass of water in tank when it is full is as follows.

Mass =
`Density * final volume`

=
`1000 * 4`

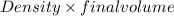
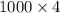
= 4000 kg

So, net mass of the fluid to be filled is as follows.

Net mass to be filled = Final mass - initial mass

= 4000 kg - 2000 kg

= 2000 kg

Mass flow rate
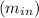`(m_(in))` = 6.33 kg/s

Mass flow rate
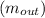`(m_(out))` = 3.25 kg/s

Time needed to fill tank =
`\frac{\text{net mass to be filled}}{\text{net difference of flow rates}}`

=
`(2000 kg)/(m_(in) - m_(out))`

=
`(2000 kg)/(6.33 kg/s - 3.25 kg/s)`

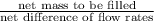
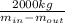
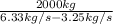
= 649.35 sec

Thus, we can conclude that 649.35 sec is taken by the tank to overflow.