Question

Considering an alloy of the two soluble components A and B. determine the masses of the alloy that are in the liquid and solid phases at a given temperature, if the total mass of alloy is 100 g, component B represents 60 % of the alloy, 25 % of the liquid is component B, and 70% of solid is component B.

Answer 1

22.22 grams of an alloy is present as liquid and 77.78 g is present as solid at given temperature.

Step-by-step explanation:

Let the mass of alloy in liquid be x and mass of alloy in solid be y.

Total mass of the alloy = 100 g

x + y = 100 g..[1]

Percentage of component B in alloy = 60%

Total Mass of component B in an alloy =
`(60)/(100)* 100 g=60 g`

25 % of the liquid is component B

Mass of component B in liquid = a

`25\%=(a)/(x)* 100`

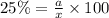
a = 0.25 x

70% of solid is component B.

Mass of component B in liquid = b

`70\%=(b)/(y)* 100`

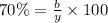
b = 0.7 y

a + b = 60

0.25 x+ 0.7 y= 60 g...[2]

On solving equation [1] and [2] , we get:

x = 22.22 g

y = 77.78 g