Answer:
Spring constant:
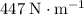 .
.
Work done:
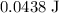 .
.
Step-by-step explanation:
Convert all values to SI units.
- Length change:
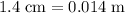 ;
; - Mass of the weight:
 .
.
Assume that the spring-mass system is vertical and is placed on the surface of the earth. The gravitational acceleration constant will be equal to
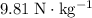 .
.
Gravitational pull on the weight:
 .
.
That's also the size of the force on the spring.
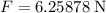 .
.
The spring constant is the size of the force required to deshape the spring (by stretching, in this case) by unit length.
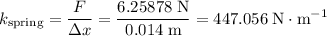 .
.
Assume that there's no energy loss in this process. The work done on the spring is the same as the elastic potential energy that it gains:
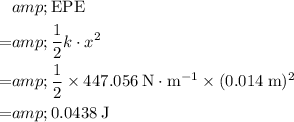 .
.