Question

Two moles of a monatomic ideal gas are contained at a pressure of 1 atm and a temperature of 300 K; 34,166 J of heat are transferred to the gas, as a result of which the gas expands and does 1216 J of work against its surroundings. The process is reversible. Calculate the final temperature of the gas.

Answer 1

Final temperature is 302 K

Step-by-step explanation:

You can now initial volume with ideal gas law, thus:

V =
`(n.R.T)/(P)`

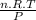
Where:

n are moles: 2 moles

R is gas constant: 0,082
`(atm.L)/(mol.K)`

T is temperature: 300 K

P is pressure: 1 atm

V is volume, with these values: 49,2 L

The work in the expansion of the gas, W, is: 1216 J - 34166 J = -32950 J

This work is:

W = P (Vf- Vi)

Where P is constant pressure, 1 atm

And Vf and Vi are final and initial volume in the expansion

-32950 J = -1 atm (Vf-49,2L) ×
`(101325 J)/(1 atm.L)`

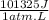
Solving: Vf = 49,52 L

Thus, final temperature could be obtained from ideal gas law, again:

T =
`(P.V)/(n.R)`

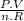
Where:

n are moles: 2 moles

R is gas constant: 0,082
`(atm.L)/(mol.K)`

P is pressure: 1 atm

V is volume: 49,52 L

T is final temperature: 302 K

I hope it helps!