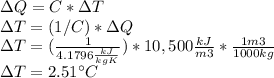Question

Two Carnot engines are operated in series with the exhaust (heat output) of the first engine being the input of the second engine. The upper temperature of this combination is 260F, the lower temperature is 40F. If each engine has the same thermal efficiency, determine the exhaust temperature of the first engine (the inlet temperature of the second engine). Ans: T = 140F 3. A nuclear power plant generates 750 MW of power. The heat engine uses a nuclear reactor operating at 315C as the source of heat. A river is available (at 20C) which has a volumetric flow rate of 165 m/s. If you use the river as a heat sink, estimate the temperature rise in the river at the point where the heat is dumped. Assume the actual efficiency of the plant is 60% of the Carnot efficiency.

Answer 1

(a) 140 F

(b) The temperature rise at the point where the heat is dumped is 2.51 degC

Step-by-step explanation:

(a) Considering T1 the temperature of input of the first engine, T2 the temperature of the exhaust of the first engine (and input of the second engine) and T3 the exhaust of the second engine, if both engines have the same efficiency we have:

`\eta=1-(T_1)/(T2)=1-(T_2)/(T_3)`

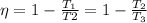
The temperatures have to be expressed in Rankine (or Kelvin) degrees

`1-(T_1)/(T2)=1-(T_2)/(T_3)\\\\(T_1)/(T2)=(T_2)/(T_3)\\\\(T_2)^(2) =T_1*T_3\\\\T_2=√(T_1*T_3) =√((459.67+260)*(459.67+40))= √(719.67*499.67)\\\\ T_2=599 \, R= (599-459.67) ^(\circ) F=140^(\circ) F`

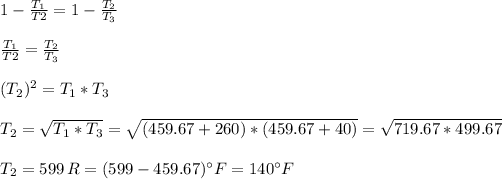
(b) The Carnot efficiency of the cycle is

`\eta_(c)=1-Th/Ts=1-(273+20)/(273+315)=0.502`

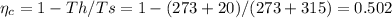
If the efficiency of the plant is 60% of the Carnot efficiency, we have

`\eta=0.6*\eta_(c)=0.6*0.502=0.302`

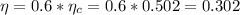
The heat used in the plant can be calculated as

`Q_i=W/\eta=750MW/0.302=2483MW`

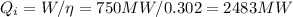
And the heat removed to the heat sink is

`Q_o=Qi-W=2483-750=1733MW`

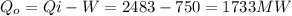
If the flow of the river is 165 m3/s, the heat per volume in the sink is

`(Q_o)/(f) =(1733 MJ/s)/(165 m3/s)= 10.5MJ/m3`

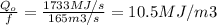
Considering a heat capacity of water C=4.1796 kJ/(kg*K) and a density ρ of 1000 kg/m3, the temperature rise of the water is

`\Delta Q=C*\Delta T\\\Delta T=(1/C)*\Delta Q\\\Delta T=((1)/(4.1796(kJ)/(kgK) ) )*10,500(kJ)/(m3)*(1m3)/(1000kg)\\\Delta T= 2.51 ^(\circ)C`