Question

A worker is told her chances of being killed by a particular process are 1 in every 300 years. Should the worker be satisfied or alarmed? What is the FAR (assuming normal working hours) and the deaths per person per year? What should her chances be, assuming an average chemical plant?

Answer 1

(a) Yes, he should be worried. The Fatal accident rate (FAR) is too high according to standars of the industry. This chemical plant has a FAR of 167, where in average chemical plants the FAR is about 4.

(b) FAR=167 and Death poer person per year = 0.0033 deaths/year.

(c) The expected number of fatalities on a average chemical plant are one in 12500 years.

Step-by-step explanation:

Asumming 50 weeks of work, with 40 hours/week, we have 2000 work hours a year.

In 300 years we have 600,000 hours.

With these estimations, we have (1/600,000)=1.67*10^(-6) deaths/hour.

If we have 2000 work hours a year, it is expected 0.0033 deaths/year.

`1.67*10^(-6) (deaths)/(hour)*2000 (hours)/(year)=0.0033 deaths/year`

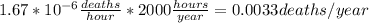
The Fatal accident rate (FAR) can be expressed as the expected number of fatalities in 100 millions hours (10^(8) hours).

In these case we have calculated 1.67*10^(-6) deaths/hour, so we can estimate FAR as:

`FAR=1.67*10^(-6) (deaths)/(hour)*10^(8)  hours=1.67*10^(2) =167`

A FAR of 167 is very high compared to the typical chemical plants (FAR=4), so the worker has reasons to be worried.

If we assume FAR=4, as in an average chemical plant, we expect

`4(deaths)/(10^(8) hour) *2000(hours)/(year)=8*10^(-5) (deaths)/(year)`

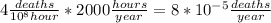
This is equivalent to say

`(1)/(8*10^(-5) ) (years)/(death)=1.25*10^(4) (years)/(death) =12500 \, (years)/(death)`

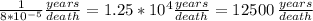
The expected number of fatalities on a average chemical plant are one in 12500 years.