Answer:
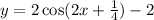
or
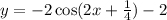
Explanation:
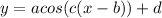 has:
has:
1) amplitude=|a|
2) phase shift=b
3) period=2pi/c
d) vertical shift=d
--------------------------------------------------
You are given the amplitude is 2. This means a could either be 2 or -2.
You are given phase shift is -1/8. This means b is -1/8.
You are given the period is pi. So we need to solve pi=2pi/c.
pi=2pi/c
Dividing both sides by pi gives:
1=2/c
Multiply both sides by c gives:
c=2
The vertical shift is -2 so d=-2.
The equation could either be:
y=2cos(2(x-(-1/8)))-2
or
y=-2cos(2(x-(-1/8)))-2
Simplifying a little gives:
y=2cos(2x+1/4)-2
y=-2cos(2x+1/4)-2