Answer:
The density of the objects in increasing order is given as C B A D.
Step-by-step explanation:
Density is the property of mater which compares amount of mater of an object and volume of an object.
The density is given by the formula:

Where,
‘ρ’ is density
‘m’ is mass of an object
‘V’ is volume of an object
Object A:
Take object A of 100 g object with a volume of 25 cubic centimetres:
We know that,
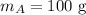 and
and
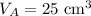
Density of A is:
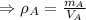
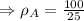

Object B:
Take object A 200 g object with a volume of 100 cubic centimetres:
We know that,
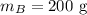 and
and
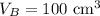
Density of B is:
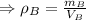
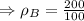
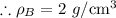
Object C:
Take object A 100 g object with a volume of 100 cubic centimetres:
We know that,
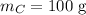 and
and
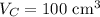
Density of C is:
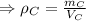
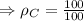

Object D:
Take object A 400 g object with a volume of 50 cubic centimetres:
We know that,
 and
and
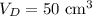
Density of object D is:
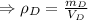
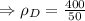
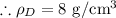
From the above calculation, on comparing,
