Step-by-step explanation:
It is known that
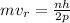
where, m = mass of the electron
r = radius of the orbit
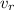 = orbital speed of the electron
= orbital speed of the electron
Equation when the electron is experiencing uniform circular motion is as follows.
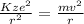 ........ (1)
........ (1)
Rearranging above equation, we get the following.
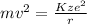
Also, v =
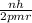 .......... (2)
.......... (2)
Putting equation (2) in equation (1) we get the following.
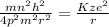
Hence, formula for radius of the nth orbital is as follows.
![r_(n) = [(h^(2))/(4p^(2)mKze^(2))]n^(2)](https://img.qammunity.org/2020/formulas/chemistry/college/2qrd8j0eo1dakph9hf08p9znrwzf3la3uh.png)
![r_(n) = [5.29 * 10^(-11)m] * (6)^(2)](https://img.qammunity.org/2020/formulas/chemistry/college/b872br4dtz1l0o4xm3vloaqe9ev2g2ok9u.png)
=
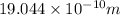
=
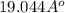
Thus, we can conclude that the value for the radius r for a n= 6 Bohr orbit is
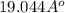 .
.