Question

Which ordered pairs are solutions to the inequality V – 2x <

-3?
Select each correct answer.

Answer 1

The solutions presented in the choice are (5,-3) and (1,-1).

Explanation:

You could plug the points in and see which satisfies the inequality (makes the inequality true).

So the inequality is:

`y-2x \le -3`

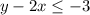
Let's check (x,y)=(0,-2):

`-2-2(0) \le -3`

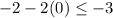
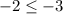`-2 \le -3` is false since -2 is more than -3.

Let's check (x,y)=(-6,-3):

`-3-2(-6) \le -3`

`-3+12 \le -3`

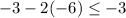
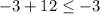
`9 \le -3` is false since 9 is more than -3.

Let's check (x,y)=(5,-3):

`-3-2(5) \le -3`

`-3-10 \le -3`

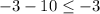
`-13 \le -3` is true.

Let's check (x,y)=(7,12):

`12-2(7) \le -3`

`12-14 \le -3`

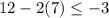
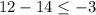
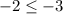`-2 \le -3` is false since -2 is more than -3.

Let's check (x,y)=(1,-1):

`-1-2(1) \le -3`

`-1-2 \le -3`

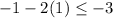
`-3 \le -3` is true since -3=-3.

So the solutions presented in the choice are (5,-3) and (1,-1).