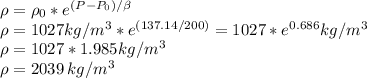Question

Sea water's density can be calculated as a function of the compressibility, B, where p = po exp[(p - Patm)/B]. Calculate the pressure and density 10,000 m below the surface of the sea. Assume ß = 200 Mega Pa.

Answer 1

The pressure 10,000 m below the surface of the sea is 137.14 MPa.

The density 10,000 m below the surface of the sea is 2039 kg/m3

Step-by-step explanation:

P0 and ρ0 are the pressure and density at the sea level (atmosferic condition). As the depth of the sea increases, both the pressure and the density increase.

We can relate presure and density as:

`(dP)/(dy)=\rho*g=\rho_0*g*e^{(P-P_0)/\beta\\\\`

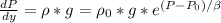
Rearranging

`(dP)/(e^((P-P_0)/\beta))= \rho_0*g*dy\\\\\int\limits^(P)_(P_0) {e^(-(P-P_0)/\beta)}dP =\int\limits^y_0 {\rho_0*g*dy}\\\\(-\beta*e^(-(P-P_0)/\beta))-(\beta*e^0)=\rho_0*g*(y-0)\\\\-\beta*(e^(-(P-P_0)/\beta)-1)=\rho_0*g*y\\\\e^(-(P-P_0)/\beta)=1-(\rho_0*g*y)/(\beta)\\\\-(P-P_0)/(\beta)  =ln(1-(\rho_0*g*y)/(\beta))\\\\P-P_0=-\beta*ln(1-(\rho_0*g*y)/(\beta))\\`

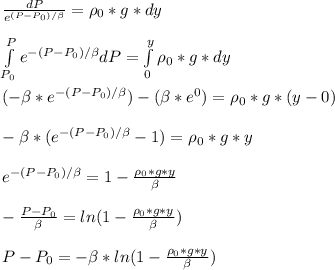
With this equation, we can calculate P at 10,000 m below the surface:

`P-P_0=-\beta*ln(1-(\rho_0*g*y)/(\beta))\\\\P-P_0=-200MPa*ln(1-(1027kg/m^3*9.81m/s^2*10,000m)/(200MPa))\\\\P-P_0=-200MPa*ln(1-(1027*9.81*10,000Pa)/(200*10^6Pa))\\\\P-P_0=-200MPa*ln(1-0.5037)\\\\P-P_0=-200MPa*(-0.6857)=137.14MPa`

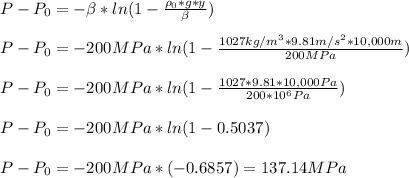
The density at 10,000 m below the surface of the sea is

`\rho=\rho_0*e^((P-P_0)/\beta)\\\rho=1027kg/m^3*e^((137.14/200))=1027*e^(0.686)kg/m^3\\\rho=1027*1.985 kg/m^3\\\rho=2039\,kg/m^3`