Answer:
(a) 8.3 g (b) 2.8 g (c) 0.0 g
Step-by-step explanation:
We can express a decay model as
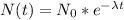
(N(t) is the grams of Radon in time t, N0 is the initial grams at t=0, lambda is the decay parameter, that we have to calculate.
With the half life period, we know that in 3.8 days we will have half the initial amount of Radon
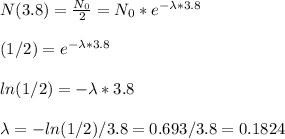
Now we have the model

(a) In one day the amount of radon will be 8.3 grams
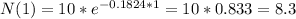
(b) In one week the amount of radon will be 2.8 grams
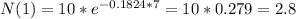
(c) In one year the amount of radon will be 0.0 grams
