Question

A company makes a profit of $50 per software program and $35 per video game. The company can produce at most 200 software programs and at most 300 video games per week. Total production cannot exceed 425 items per week. How many items of each kind should be produced per week in order to maximize the profit?

Use linear programming to solve. Show all your work.

Answer 1

The number of software programs per week to maximize the profit should be 200 and the number of video games per week to maximize the profit should be 225

Step-by-step explanation:

Let

x ----> the number of software programs per week to maximize the profit

y ----> the number of video games per week to maximize the profit

we know that

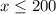`x \leq 200` ---> inequality A

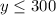`y \leq 300` ---> inequality B

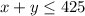`x+y \leq 425` ---> inequality C

Remember that

The profit P is equal to

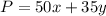`P=50x+35y` ----> equation D

Solve the system of inequalities by graphing

The solution is the shaded area

see the attached figure

The vertices of the shaded area are

(0,0), (125,300),(200,225),(200,0)

Substitute the value of x and the value of y of each vertices in the equation D (Profit) to determine how many items of each kind should be produced per week in order to maximize the profit

For (0,0) ---->
`P=50(0)+35(0)=\$0`

For (125,300) ---->
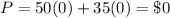
`P=50(125)+35(300)=\$16,750`

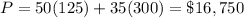
For (200,225) ---->
`P=50(200)+35(225)=\$17,875`

For (200,0) ---->
`P=50(200)+35(0)=\$10,000`

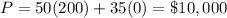
therefore

The point that maximize the profit is (200,225)

The number of software programs per week to maximize the profit should be 200 and the number of video games per week to maximize the profit should be 225