The text looks incomplete. Here the complete question found on google:
"The acceleration of a bus is given by ax(t)=αt, where α = 1.28m/s3 is a constant. Part A If the bus's velocity at time t1 = 1.13s is 5.09m/s , what is its velocity at time t2 = 2.02s ? If the bus's position at time t1 = 1.13s is 5.92m , what is its position at time t2 = 2.02s ?"
A) 6.88 m/s
The velocity of the bus can be found by integrating the acceleration. Therefore:
 (1)
(1)
where
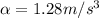
C is a constant term
We know that at
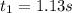 , the velocity is
, the velocity is
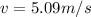 . Substituting these values into (1), we can find the exact value of C:
. Substituting these values into (1), we can find the exact value of C:
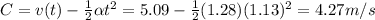
So now we can find the velocity at time
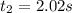 :
:
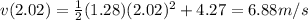
B) 11.2 m
To find the position, we need to integrate the velocity:
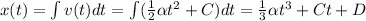 (2)
(2)
where D is another constant term.
We know that at
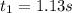 , the position is
, the position is
 . Substituting these values into (2), we can find the exact value of D:
. Substituting these values into (2), we can find the exact value of D:

And so now we can find the position at time
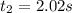 using eq.(2):
using eq.(2):
