Question

The Reynolds number, Re, is a dimensionless number used to characterize different flow regimes in a fluid. The Reynolds number can be defined as DVp Re= where D is the diameter of the pipe, Vis the mean fluid velocity, pis the density of the fluid, and pis the dynamic viscosity of the fluid. What is the Reynolds number of blood leaving the heart through the aorta if it has a dynamic viscosity of u 3.40 cP (centipoise), a density of p 1043 kg/m, travels at a mean fluid velocity of V= 32.9 cm/s, and the diameter of the aorta is D = 1.85 cm?

Answer 1

The aswer is Re= 1867.123

Step-by-step explanation:

You know that Reynolds is:

`Re=(p*v*D)/(u)`

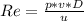
But the units of p, v, D and u must be in the same reference system. This means that you must handle the same units. So, you must do the corresponding unit conversions . Usually The International System of Units is used, where:

the density p is measured in
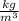`(kg)/(m^(3) )` the velocity v in
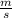`(m)/(s)`, the diameter in m (meters) and the viscosity in
`(kg)/(m*s)`

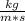
But you can choice other system of units.

The density, in this case, is expressed in
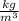`(kg)/(m^(3) )` ( Note that in the statement the data appears as kg / m. But remember that this isn't possible because density is the amount of mass in a given volume. You can assume that the given data is
`(kg)/(m^(3) )`).

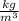For density then you shouldn't convert units, because it respects the International System of Units.

The velocity is expressed in
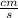`(cm)/(s)`. So, you must change these units to
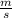`(m)/(s)`. For that, The Rule of Three is usually used, where it is known that 1 cm is 0.01 cm. So:

1 cm ⇒ 0.01 m

32.9 cm ⇒ x

`x=(32.9*0.01)/(1)`

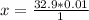
Finally the velocity is: 0.329
`(m)/(s)`

In the same way, you can convert the units of the diameter.

1 cm ⇒ 0.01 m

1.85 cm ⇒ x

`x=(1.85*0.01)/(1)`

The diameter is: 0.0185 m

Finally, you must convert the viscosity units, applying The Rule of Three:

1 cP ⇒ 0.001
`(kg)/(m.s)`

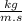
3.40 cP ⇒ x

`x=(3.4*0.001)/(1)`

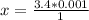
So, the viscosity is: 0.0034
`(kg)/(m*s)`

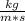
Now, with all units in the same system, you can calculate the Reynolds number.You just have to replace the numbers in the definition and verify that the Reynolds is a dimensionless number.

`Re=(p*v*D)/(u) =(1043*0.329*0.0185)/(0.0034)`

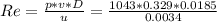
Re= 1867.123

Unit Verification:

`Re=((kg)/(m^(3) ) *(m)/(s)  *m)/((kg)/(m*s) )`

By simple simplification, adimensionality can be observed.