Question

In a rectangle FGHI, diagonals FH and GI intersect at E
What is the length of FH?

Answer 1

The length of
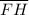`\overline {FH}` is;

D. 38 units

Explanation:

The given parameters are;

The type of the given quadrilateral FGHI = Rectangle

The diagonals of the quadrilateral =
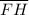`\overline {FH}` and
`\overline {GI}`

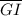
The length of IE = 3·x + 4

The length of EG = 5·x - 6

We have from segment addition postulate,
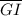`\overline {GI}` = IE + EG

The properties of a rectangle includes;

1) Each diagonal bisects the other diagonal into two

Therefore,
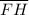`\overline {FH}` bisects
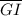`\overline {GI}`, into two equal parts, from which we have;

IE = EG

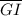`\overline {GI}` = IE + EG

3·x + 4 = 5·x - 6

4 + 6 = 5·x - 3·x = 2·x

10 = 2·x

∴ x = 10/2 = 5

From which we have;

IE = 3·x + 4 = 3 × 5 + 4 = 19 units

EG = 5·x - 6 = 5 × 5 - 6 = 19 units

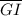`\overline {GI}` = IE + EG = 19 + 19 = 38 units

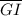`\overline {GI}` = 38 units

2) The lengths of the two diagonals are equal. Therefore, the length of segment
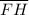`\overline {FH}` is equal to the length of segment
`\overline {GI}`

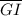
Mathematically, we have;

`\overline {FH}` =
`\overline {GI}` = 38 units

∴
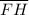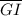`\overline {FH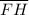}` = 38 units.