What is the heat of vaporization of ethanol, given that ethanol has a normal boiling point of 63.5°C and the vapor pressure of ethanol is 1.75 atm at 780 g.

Question

asked Sep 17, 2020 40.5k views

1 Answer

Reem · Answer 1 · 2020-09-22T01:36:53+0000

Step-by-step explanation:

According to Clausius-Claperyon equation,

$ln ((P_(2))/(P_(1))) = \frac{-\text{heat of vaporization}}{R} * [(1)/(T_(2)) - (1)/(T_(1))]$

The given data is as follows.

T_(1) = 63.5^(o)C = (63.5 + 273) K

= 336.6 K

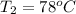T_(2) = 78^(o)C = (78 + 273) K

= 351 K

P_(1) = 1 atm,
P_(2) = ?

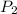Putting the given values into the above equation as follows.

$ln ((P_(2))/(P_(1))) = \frac{-\text{heat of vaporization}}{R} * [(1)/(T_(2)) - (1)/(T_(1))]$

$ln ((1.75 atm)/(1 atm)) = \frac{-\text{heat of vaporization}}{8.314 J/mol K} * [(1)/(351 K) - (1)/(336.6 K)]$

$\Delta H$ =
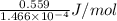
(0.559)/(1.466 * 10^(-4)) J/mol

=
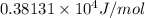
0.38131 * 10^(4) J/mol

= 3813.1 J/mol

Thus, we can conclude that the heat of vaporization of ethanol is 3813.1 J/mol.